八大排序时空复杂度表
| Method |
Average |
Worst |
Best |
Space |
Stable |
| 直接插入排序 |
$O(n^2)$ |
$O(n^2)$ |
$O(n)$ |
$O(1)$ |
稳定 |
| 希尔排序 |
$O(n^{1-2})$ |
– |
– |
$O(1)$ |
不稳定 |
| 冒泡排序 |
$O(n^2)$ |
$O(n^2)$ |
$O(n)$ |
$O(1)$ |
稳定 |
| 快速排序 |
$O(nlog_2n)$ |
$O(n^2)$ |
$O(nlog_2n)$ |
$O(log_2n)$ |
不稳定 |
| 直接选择排序 |
$O(n^2)$ |
$O(n^2)$ |
$O(n^2)$ |
$O(1)$ |
不稳定 |
| 堆排序 |
$O(nlog_2n)$ |
$O(nlog_2n)$ |
$O(nlog_2n)$ |
$O(1)$ |
不稳定 |
| 归并排序 |
$O(nlog_2n)$ |
$O(nlog_2n)$ |
$O(nlog_2n)$ |
$O(n)$ |
稳定 |
| 基数排序 |
$O(d(n+r))$ |
$O(d(n+r))$ |
$O(d(n+r))$ |
$O(n+rd)$ |
稳定 |
注:
1.希尔排序的时间复杂度和增量的选择有关。
2.基数排序的复杂度中,$r$代表关键字的基数,$d$代表长度,$n$表示关键字的个数。
下面分别介绍这些算法的简单实现,由于每种算法都有若干的优化版本,本文只列出常见的实现,若要看进阶的可以参考:力扣-排序算法全解析
另外按照算法的操作特性,可以分为比较排序和非比较排序,比较排序中的若干种排序又可以分为插入排序(直接插入排序、希尔排序)和交换排序(冒泡排序、快速排序)以及选择排序(直接选择排序、堆排序)。非比较排序有计数排序,桶排序等
参考: 各类排序算法生成与测试样例代码
直接插入排序(Direct Insert Sort)
外层循环每趟确定一个数的最终位置,内层循环每次从外层循环的位置往前寻找合适的插入位置。合适指的是,第一个顺序对的位置即满足nums[j-1] < nums[j]的j的位置
1
2
3
4
5
6
7
8
9
10
|
vector<int> insert_sort(vector<int>& nums) {
for (int i = 1; i < nums.size(); ++i) {
int j = i;
while (j >= 1 && nums[j] < nums[j - 1]) {
swap(nums[j], nums[j - 1]);
--j;
}
}
return nums;
}
|
希尔排序(Shell Sort)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
vector<int> shell_sort(vector<int>& nums) {
// 找到符合条件的knuth序列的最大值
int max_knuth_num = 1;
while (max_knuth_num <= nums.size() / 3) {
max_knuth_num = max_knuth_num * 3 + 1;
}
// 增量按照 Knuth 序列规则依次递减
for (int gap = max_knuth_num; gap > 0; gap = (gap - 1) / 3) {
// 从gap开始遍历到结尾,=
for (int i = gap; i < nums.size(); ++i) {
int cur_num = nums[i];
int pre_index = i - gap;
// 对每个当前遍历的点cur_num,使用插入排序从后往前调整其前面的间隔序列
while (pre_index >= 0 && cur_num < nums[pre_index]) {
// 向后挪动位置
nums[pre_index + gap] = nums[pre_index];
pre_index -= gap;
}
// 坐下来
nums[pre_index + gap] = cur_num;
}
}
return nums;
}
|
冒泡排序(Bubble Sort)
外层循环每次确定一个数的最终位置,内层循环从头开始每次比较相邻的两个数,大的往后冒泡,内层循环结束后,当前遍历集合的最大数已经“冒泡”到了末尾。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
vector<int> bubble_sort(vector<int>& nums) {
bool swapped;
for (int i = 1; i < nums.size(); ++i) {
swapped = false;
for (int j = 1; j < nums.size() - i + 1; ++j) {
if (nums[j] < nums[j - 1]) {
swap(nums[j], nums[j - 1]);
swapped = true;
}
}
if (!swapped) break;
}
return nums;
}
|
快速排序(Quick Sort)
快速排序使用了递归操作,所以其空间复杂度有所增加,但是时间复杂度更占据优势,也是其名字的由来。快速排序不适合已经大部分有序的情况,这样会增加遍历操作,甚至时间复杂度上升至$O(n^2)$ 。考虑这种情况,我们在每次划分的时候随机选择一个数进行交换,可以使得数组更混乱。
其思想是,每一趟排序确定一个数的最终位置,在该位置上,左边的数都小于该数,右边的数都大于该数,由此,我们也称这一趟排序为一次划分(partition), 每次划分时,都会不断地找到从左往右第一个比该数大的数a和从右往左第一个比该数小的数b,然后将两者交换一下,最终满足条件。在该次划分后,确定了一个数的最终位置pos,那么可以递归地对pos左边的数和pos右边的数进行划分。最后每个数都到了其实际的位置,排序就完成了。
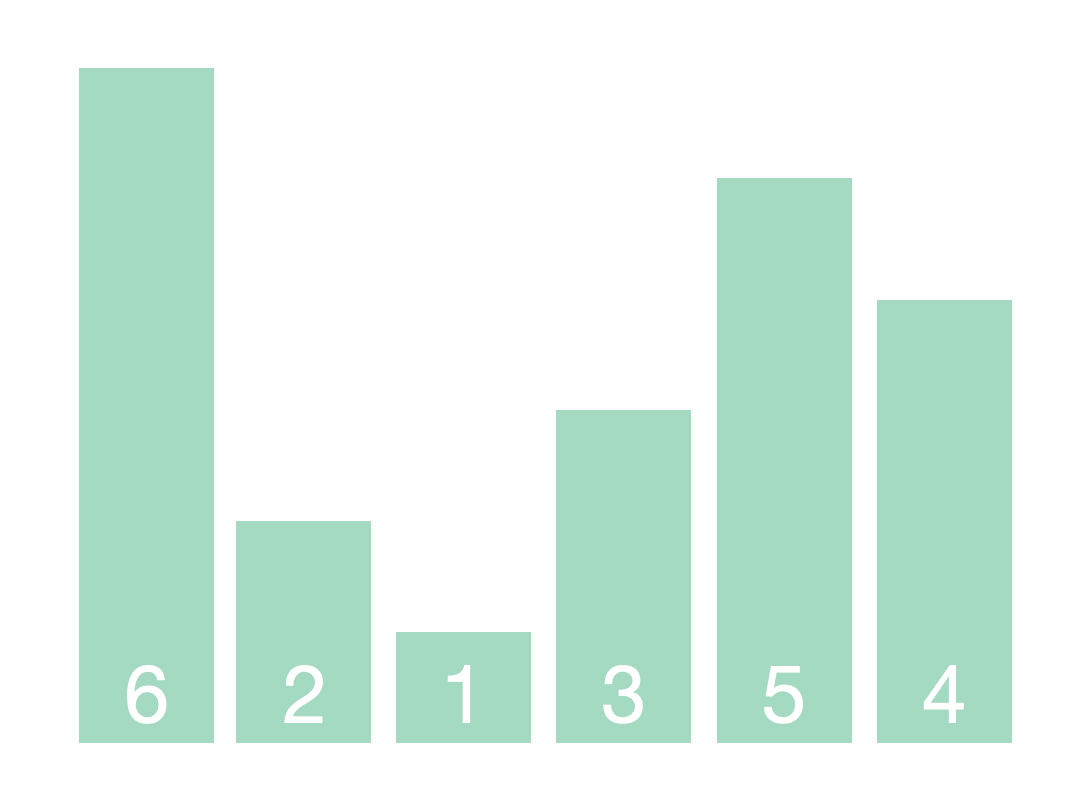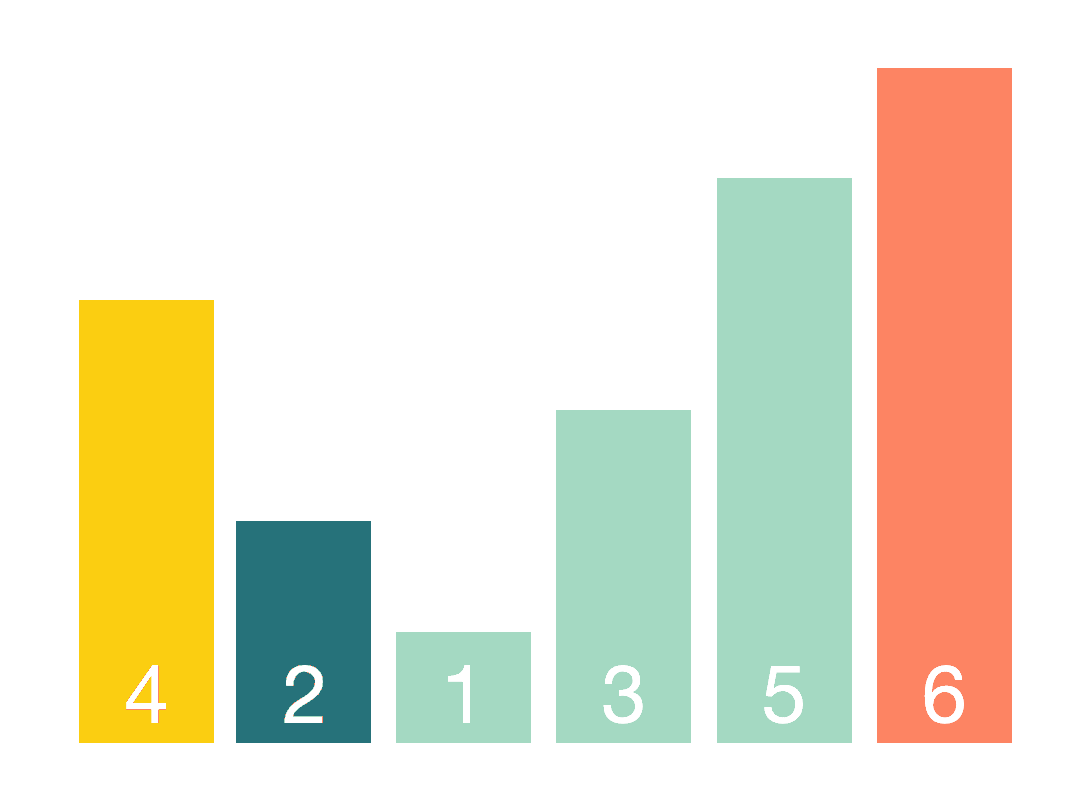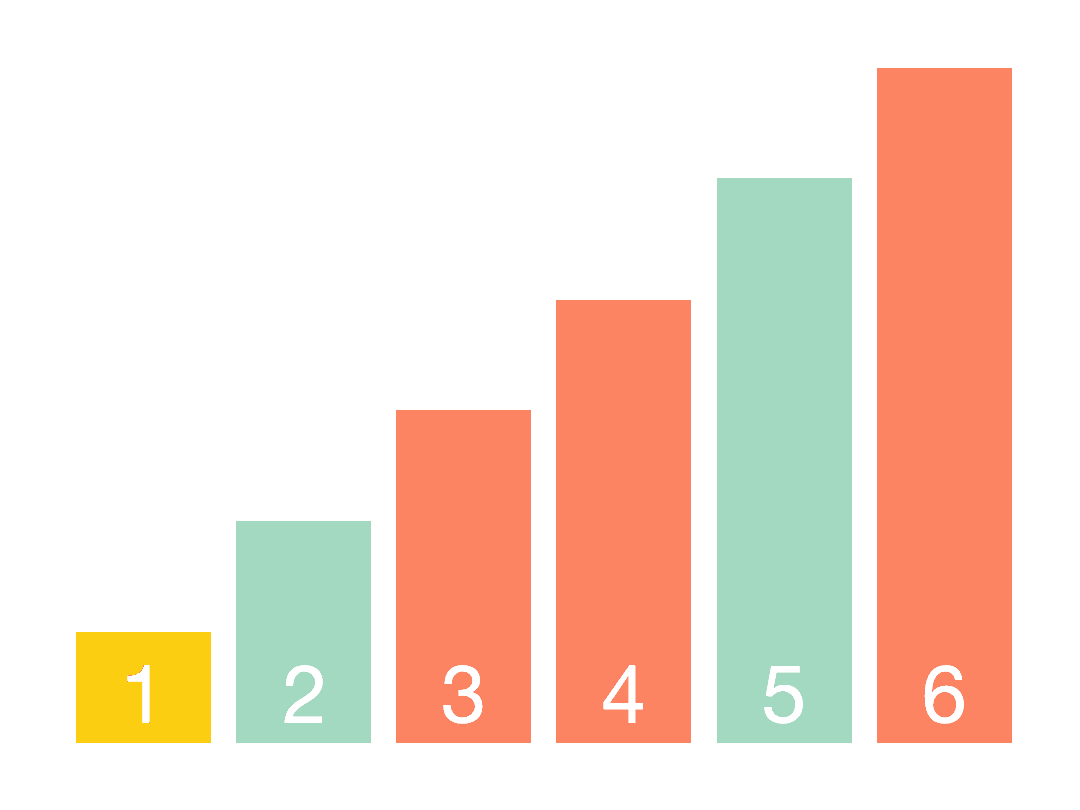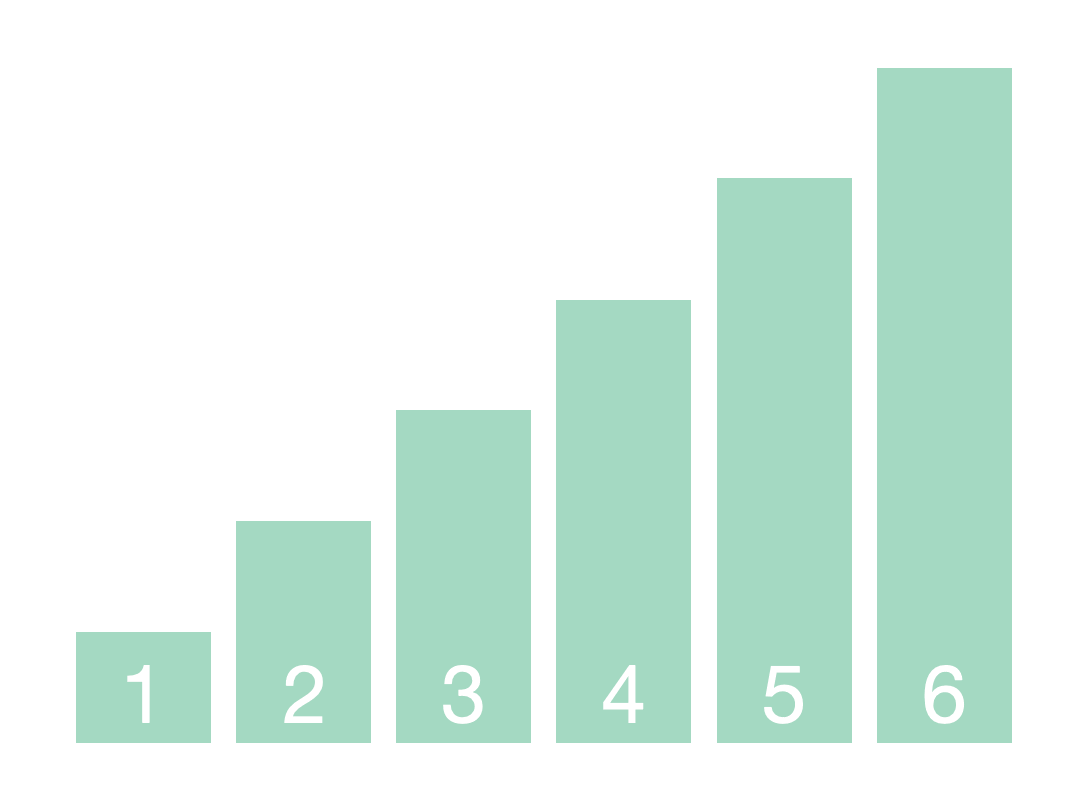
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
// 划分函数,返回已经有序的位置
int partition(vector<int>& nums, int left, int right) {
// 随机选择一个位置交换
std::random_device rd;
std::mt19937 mt(rd());
std::uniform_int_distribution<int> dist(left, right);
int pos = dist(mt);
swap(nums[left], nums[pos]);
int pivot = nums[left];
while (left < right) {
while (left < right && nums[right] > pivot) right--;
nums[left] = nums[right];
while (left < right && nums[left] <= pivot) left++;
nums[right] = nums[left];
}
nums[left] = pivot;
return left;
}
void my_qsort(vector<int>& nums, int left, int right) {
// 保证区间内至少有两个元素,left 和 right
if (left >= right) return;
int pivot_pos = partition(nums, left, right);
my_qsort(nums, left, pivot_pos - 1);
my_qsort(nums, pivot_pos + 1, right);
}
vector<int> quick_sort(vector<int>& nums) {
my_qsort(nums, 0, nums.size() - 1);
return nums;
}
|
直接选择排序(Direct Select Sort)
外层循环每次确定一个数的最终位置,内层循环每次从未定序数的集合种选出其最小值然后放到其最终的位置。
1
2
3
4
5
6
7
8
9
10
11
12
|
vector<int> select_sort(vector<int>& nums) {
for (int i = 0; i < nums.size(); ++i) {
int min_idx = i;
for (int j = i + 1; j < nums.size(); ++j) {
if (nums[j] < nums[min_idx]) {
min_idx = j;
}
}
swap(nums[i], nums[min_idx]);
}
return nums;
}
|
堆排序(Heap Sort)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
// 自顶向下调整堆
void adjust_down(vector<int>& nums, int k, int max_len) {
// 每调整一次堆,最大的元素就在第一个位置了
// int num = nums[k];
// 先使 i 指向左子元素,然后指向左右子元素中较大值
for (int i = k * 2 + 1; i < max_len; i = i * 2 + 1) {
// 左右子结点比较
if (i + 1 < max_len && nums[i] < nums[i + 1]) {
++i;
}
if (nums[i] < nums[k]) {
break;
} else {
// 子结点比当前结点大要交换一下,然后将该子结点作为下一个遍历结点
swap(nums[k], nums[i]);
k = i;
}
}
}
// 建堆,默认大顶堆
void build_heap(vector<int>& nums) {
int size = nums.size();
// 非叶子结点遍历
for (int i = size / 2; i >= 0; --i) {
adjust_down(nums, i, size);
}
}
// 堆排序, Worst: O(n^2), Best: O(n) Avg: O(nlog(n)) 稳定
vector<int> heap_sort(vector<int>& nums) {
// 从小到大,可以建大根堆,将最大元素依次取出放到后面
build_heap(nums);
for (int i = nums.size() - 1; i > 0; --i) {
// n-1趟排序,将堆顶最大元素与第i个位置元素交换,大元素就依次置后了
swap(nums[0], nums[i]);
// 重新调整堆,限制范围缩小以保护置后的大元素,从根结点调整
adjust_down(nums, 0, i);
}
return nums;
}
|
归并排序(Merge Sort)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
void my_merge_sort(vector<int>& nums, int left, int right) {
if (left >= right) return;
int mid = left + (right - left) / 2;
my_merge_sort(nums, left, mid);
my_merge_sort(nums, mid + 1, right);
int i = left, j = mid + 1, k = 0, temp[right - left + 1];
while (i <= mid && j <= right) {
temp[k++] = nums[i] <= nums[j] ? nums[i++] : nums[j++];
}
while (i <= mid) temp[k++] = nums[i++];
while (j <= right) temp[k++] = nums[j++];
for (k = 0, i = left; i <= right; ++k, ++i) {
nums[i] = temp[k];
}
}
// 归并排序, Worst: O(n^2), Best: O(n) Avg: O(nlog(n)) 稳定
vector<int> merge_sort(vector<int>& nums) {
my_merge_sort(nums, 0, nums.size() - 1);
return nums;
}
|
基数排序(Radix Sort)
下面实现的版本可以包含有负数的情况,将基数进行加9处理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
vector<int> radix_sort(vector<int>& nums) {
int max = 0;
// 找出位数最多的数
for (int num : nums) {
if (abs(num) > max) {
max = abs(num);
}
}
// 计算最长位数
int max_digit_len = 0;
while (max != 0) {
++max_digit_len;
max /= 10;
}
// 使用计数排序法对基数进行排序,下标[0, 18]对应[-9, 9]
vector<int> counting(19);
vector<int> result(nums.size());
int dev = 1;
for (int i = 0; i < max_digit_len; ++i) {
for (int num : nums) {
// 下标调整
int radix = num / dev % 10 + 9;
++counting[radix];
}
for (int j = 1; j < counting.size(); ++j) {
counting[j] += counting[j - 1];
}
// 使用倒序遍历的方式完成计数排序
for (int j = nums.size() - 1; j >= 0; --j) {
int radix = nums[j] / dev % 10 + 9;
result[--counting[radix]] = nums[j];
}
// 计数排序完成后,将结果拷贝回 nums 数组
std::copy(result.begin(), result.end(), nums.begin());
std::fill(counting.begin(), counting.end(), 0);
dev *= 10;
}
return nums;
}
|
计数排序(Counting Sort)
计数排序就是一种时间复杂度为 $O(n)$ 的排序算法,该算法于 19541954 年由 Harold H. Seward 提出。在对一定范围内的整数排序时,它的复杂度为 $O(n+k)$(其中 k 是整数的范围大小)
用到的空间主要是长度为 k 的计数数组和长度为 n 的结果数组,所以空间复杂度也是 $O(n+k)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
// 计数排序, Worst: O(n+k), k 表示数据范围大小。 本实现方式稳定
vector<int> counting_sort(vector<int>& nums) {
if (nums.size() <= 1) return{};
int max = nums[0];
int min = nums[0];
for (int i = 1; i < nums.size(); ++i) {
if (nums[i] > max) max = nums[i];
else if (nums[i] < min) min = nums[i];
}
int range = max - min + 1;
vector<int> counting(range, 0);
for (int num : nums) {
counting[num - min]++;
}
// 每个元素在结果数组中的最后一个下标位置 = 前面比自己小的数字的总数 + 自己的数量 - 1。
// 我们将 counting[0] 先减去 1,后续 counting 直接累加即可
counting[0]--;
for (int i = 1; i < range; ++i) {
counting[i] += counting[i - 1];
}
vector<int> result(nums.size());
for (int i = nums.size() - 1; i >= 0; --i) {
// counting[arr[i] - min] 表示此元素在结果数组中的下标
result[counting[nums[i] - min]] = nums[i];
// 更新 counting[arr[i] - min],指向此元素的前一个下标
counting[nums[i] - min]--;
}
for (int i = 0; i < nums.size(); ++i) {
nums[i] = result[i];
}
return nums;
}
|