假设检验
假设检验(Hypothesis testing)是推论统计中用于检验统计假设的一种方法。而“统计假设”是可通过观察一组随机变量的模型进行检验的科学假说。一旦能估计未知参数,就会希望根据结果对未知的真正参数值做出适当的推论。
统计上对参数的假设,就是对一个或多个参数的论述。而其中欲检验其正确性的为零假设,零假设通常由研究者决定,反映研究者对未知参数的看法。相对于零假设的其他有关参数之论述是备择假设(Alternative hypothesis,记为或),它通常反应了执行检验的研究者对参数可能数值的另一种(对立的)看法(换句话说,备择假设通常才是研究者最想知道的)。

假设检验步骤
- 最初研究假设为真相不明。
- 提出相关的零假设和备择假设。
- 考虑检验中对样本做出的统计假设;例如,关于总体资料的分布形式或关于独立性的假设。无效的假设将意味此检验的结果是无效的。
- 选择一个显著性水平 (α),若低于这个概率阈值,就会拒绝零假设。最常用的是 5% 和 1%。
- 选择适合的检验统计量(Test statistic)T。
- 在设定零假设为真下推导检验统计量的分布。在标准情况下应该会得出一个熟知的结果。比如检验统计量可能会符合正态分布或学生t-分布。
- 根据在零假设成立时的检验统计量T分布,找到概率为显著性水平 (α)的区域,此区域称为“拒绝域”(记作RR或CR),即在零假设成立的前提下,落在拒绝域的概率只有α。
- 针对检验统计量T,根据样本计算其估计值tobs。
- 若估计值tobs未落在拒绝域,则“不拒绝”零假设(do no reject )。若估计值tobs落在拒绝域,则拒绝零假设,接受备择假设。
要注意的是一般不会将检验结果称作“接受”零假设,而是因没有显著证据证明零假设为非,所以“不拒绝”零假设。
相关概念
原假设
也称为零假设(Null Hypothesis),即为你要对其进行检验的断言,除非有足够的证据进行反驳,否则你将接受这个断言。用符号$H_0$表示
备择假设
与原假设对立的断言称为备择假设(Alternative hypothesis),用$H_1$ 表示,如果有足够的证据拒绝$H_0$ ,我们就接受$H_1$
二者不必涵盖所有可能结果
进行假设检验时,你假定原假设为真;如果有足够证据反驳原假设,则拒绝原假设,接受备择假设
我们根据原假设$H_0$ 选择检验统计量
我们需要检验是否有充足的证据反驳原假设。办法是:首先假设$H_0$ 为真,然后寻找不利于$H_0$ 的证据。先看看得出原假设观察结果的可能性多大。也就是说,取样本结果,然后计算发生这个结果的概率——通过求拒绝域实现这个目标
拒绝域
假设检验的拒绝域是一组数值,这组数值给出反驳原假设的最极端证据
问题是:当这些证据的强度达到多大时,我们能够坚决地拒绝原假设?我们需要通过某种方法指出何时能够合理地拒绝原假设——指定一个拒绝域即可实现这一目的
临界值(“c”):我们把拒绝域的分界点称为临界值
为了求出假设检验的拒绝域,首先需要定下“显著性水平”。
显著性水平($\alpha$)
检验的显著性水平所量度的是一种愿望,即希望在样本结果的不可能程度达到多大时,就拒绝原假设$H_0$ ,像置信区间的置信水平一样,显著性水平用百分数表示
显著性水平常用希腊字母 $\alpha$ 表示,$\alpha$ 越小,为了拒绝 $H_0$ ,样本结果需要达到的不可能程度越高
单尾检验:即检验的拒绝域落在数据集的一侧,如果备择假设包括一个<符号,则使用左尾,此时拒绝域位于数据的的极端,>符号则相反
双尾检验:即拒绝域一分为二位于数据集的两侧,你选择检验水平 $\alpha$ ,然后将拒绝域一分为二,并确保整个拒绝域以相应的概率反映这个检验水平。两侧各占 $\alpha/2$ ,因此总和为$\alpha$
$p$ 值
即某个小于或者等于拒绝域方向上的一个样本数值的概率。具体求法是利用样本进行计算,然后判定样本结果是否落在假设检验的拒绝域以内,也就说我们通过 $p$ 值确定是否拒绝原假设,$p$ 值小于显著性水平 $\alpha$,拒绝原假设。
已经求得P值的情况下,可以用它来检查我们的样本是否落在拒绝域内。以显著性水平5%的左尾检验为例,这意味着,如果 $p$ 值小于0.05,就能拒绝零假设。
检验统计量:检验统计量就是用于进行检验的变量
一旦确定了检验的显著性水平,就无法改变
第一类错误: 错误地拒绝原假设
第二类错误:错误地接收原假设
发生第一类错误的概率等于你的结果位于拒绝域以内的概率。由于拒绝域由检验水平决定,说明如果检验的显著性水平为$\alpha$ , 则发生第一类错误的概率必须也等于$\alpha$ ,即:
$$ P(第一类错误)=\alpha $$
其中 $\alpha$ 为检验的显著性水平
发生第二类错误的概率要比求第一类错误的概率难得多,其通常用希腊字母$\beta$ 表示,
$$ P(第二类错误)=\beta $$
求解步骤如下:
-
检查是否拥有 $H_1$ 的特定数值
没有这个数值则无法计算第二类错误概率
-
求检验拒绝域以外的数值范围
假设检验统计量已经标准化,则该数值范围要进行逆标准化
-
假定 $H_1$ 为真,求得到这些数值的概率
也就是说,我们要求出得到拒绝域以外的数值的概率,但这一次用 $H_1$ 而不是 $H_0$ 对检验统计量进行描述
只有在备择假设具有唯一特定值时才能计算第二类错误的发生概率
假设检验的功效即你正确地拒绝一个假原假设的概率
$$ 功效=1-\beta $$
方差已知情况下求均值是Z检验。 方差未知求均值是 $t$ 检验(样本标准差 $s$ 代替总体标准差 $\sigma$,由样本平均数推断总体平均数) 均值方差都未知求方差是 $\chi^2$检验 两个正态分布样本的均值方差都未知情况下求两个总体的方差比值是 $F$ 检验。
Z检验
Z检验量(Z-statistic)
$$ Z=\frac{\overline{X}-\mu_{\overline{x}}}{\sigma/\sqrt{n}}=\frac{\overline{X}-\mu_{\overline{x}}}{s/\sqrt{n}} $$
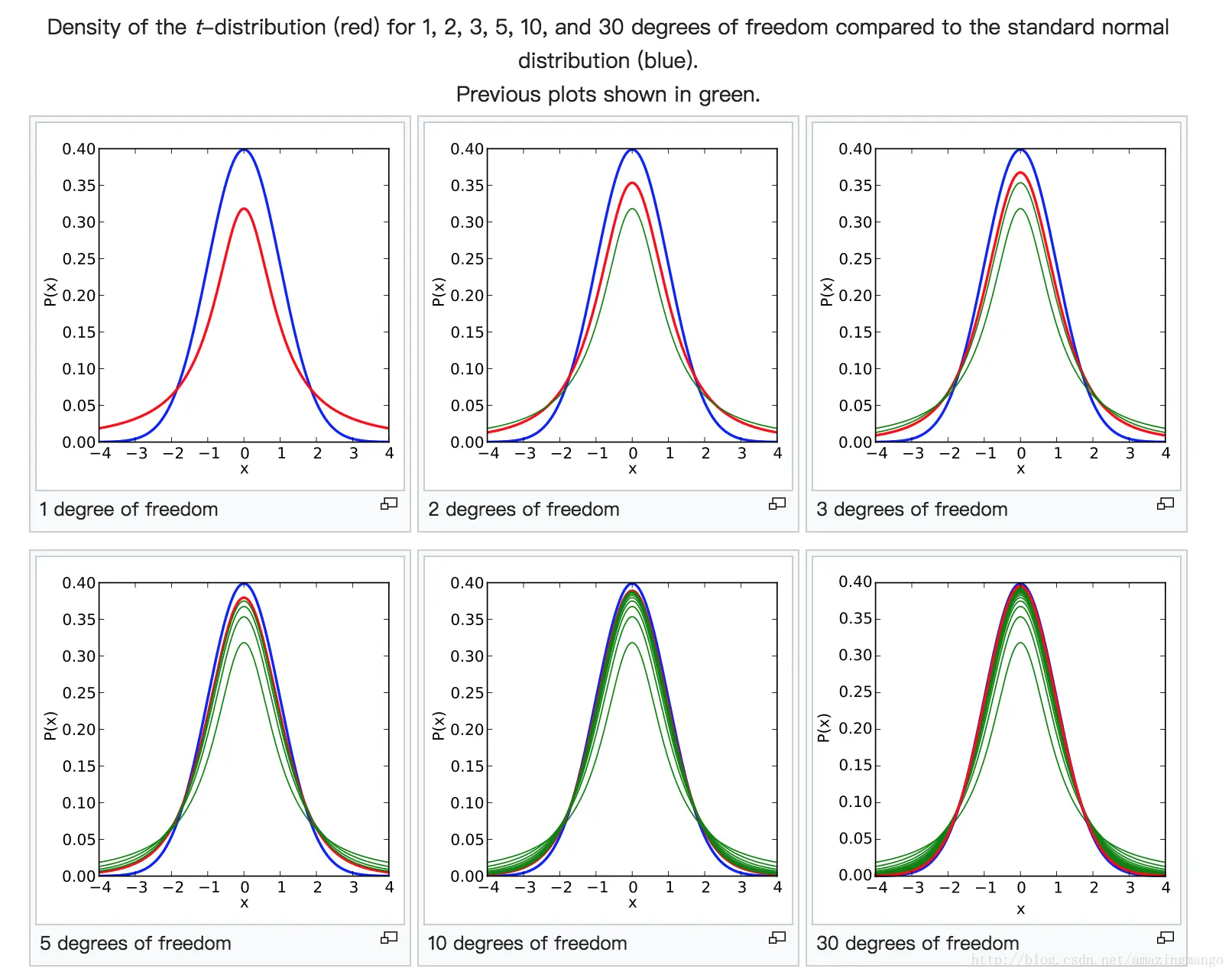
当 $n$ 大于等于30时,其分布接近正态分布,否则其分布为 $t $ 分布,因为当样本容量较大时,我们可以通过样本标准差来估计总体标准差,这样相当于总体方差已知。而样本容量较小时,我们不能通过样本来估计总体方差,这时相当于总体方差未知,属于 $t $ 分布
实例
制药公司宣称他们的新药能够在两周内治愈90%的打鼾患者,外科诊所医生决定对药物进行试验,验证制药公司的说法是否可信,他随机抽取了100名患者,用该药进行了两周的治疗后,有80个人被治愈。现在要通过这个样本来对制药公司的断言进行 $Z$ -检验
-
确定假设
$H_0:p=0.9, H_1:p<0.9 $ 即原假设为治愈率为90%,备择假设为治愈率小于90%
-
选择检验统计量
原分布为二项分布,当样本容量较大时,可以用正态分布近似代替二项分布,此时有$X\sim{N(np,npq)}$
例子中有 $X\sim{N(90,9)}$
经过标准化得到,$Z=\frac{X-90}{\sqrt9}=\frac{X-90}{3}$
也就是说,我们的统计量可以是$Z=\frac{X-90}{3} ,Z\sim{N(0,1)}$ ,我们将$Z$作为统计量是因为通过它可以轻松查出概率,进而了解在以制药公司断言为前提下,我们的样本结果的不可能程度如何。我们将80代入$X$,这样就能求出治愈人数为80或以下的概率
-
求出拒绝域
有了检验统计量后我们还要求拒绝域。由于我们的备择假设为 $p<0.9$ ,这表明拒绝域位于左尾,拒绝域还取决与显著性水平,这里取显著性水平为5%
由于$Z$ 统计量符合标准正态分布,于是可以用概率表查出临界值 $c$。
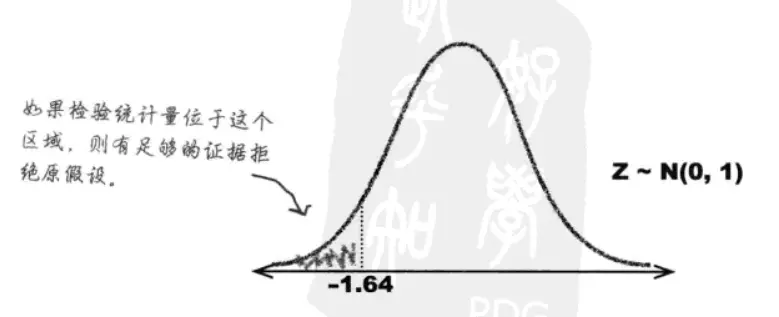
由于我们的显著性水平为5%,于是临界值 $c$ 等于令 $P(Z<c)=0.05$ 的数值,通过概率表可以查到该值为-1.64
这说明只要检验统计量小于-1.64,我们就有足够的证据拒绝原假设

-
求出p值
拒绝域位于分布的左尾,治愈人数为80,那么80对应的Z 值为(80-90)/3=-3.33
$p$ 值算法为 $P(Z<z)=P(Z<-3.33)$
-
查看检验统计量是否位于拒绝域内
如果 $p$ 值小于0.05(显著性水平),则检验统计量位于拒绝域中,此例中,检验统计量为0.0004,明显位于拒绝域中
-
做出决策
拒绝原假设
t检验
T检验是用于两个样本(或样本与群体)平均值差异程度的检验方法。它是用T分布理论来推断差异发生的概率,从而判定两个平均数的差异是否显著。
T检验的适用条件为样本分布符合正态分布。 T检验的应用条件:
- 当样本例数较小时,要求样本取自正态总体;
- 做两样本均数比较时,还要求两样本的总体方差相 等。
T检验的用途:(1)样本均数与群体均数的比较;(2)两样本均数的比较。
t检验例子
- 样本与总体均值的比较
大量检测已知正常人血浆载脂蛋白 $E(apo E)$ 总体平均水平为 $4.15mmol/L$。某医师经抽样测得41例陈旧性心机梗死患者的血浆载脂蛋白E平均浓度为 $5.22mmol/L$,标准差为$1.61mmol/L$。据此能否认为陈旧性心肌梗死患者的血浆载脂蛋白$E$平均浓度与正常人的平均浓度不一致?
- 建立检验假设和确定检验水准。
$H_0: \mu=\mu_0,H1: \mu≠\mu_0,\alpha=0.05$,双侧检验;
- 选定检验方法和计算统计量。用单样本的t检验,
$$ t=\frac{\overline{x}-\mu_0}{s_{\overline{x}}}=\frac{\overline{x}-\mu_0}{s/\sqrt{n}}=\frac{5.22-4.15}{1.61/\sqrt{41}}=4.26 $$
自由度 $v=41-1=40$
-
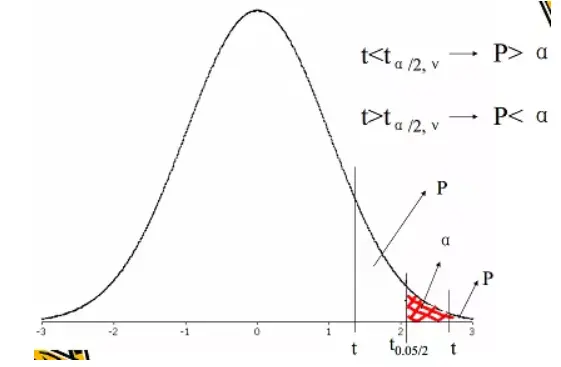
确定P值和作出推断结论。
查 $t$ 分布表,$ t_{0.05/2,40}=2.021$, $ t=4.26>t_{0.05/2, 40}$,$P<0.05$。按 $\alpha=0.05 $水准,拒绝 $H_0$,接受 $H_1$,可认为陈旧性心肌梗死患者的血浆载脂蛋白$E$平均浓度与正常人的差别有统计学意义,结合专业可以认为前者平均浓度较高。

- 配对设计定量资料的 $t$ 检验
• 配对设计的 $t$ 检验研究的是差值均数(样本均数)与理论上的差值总体均数的比较。
• 首先计算出各对差值 $d$ 的均数。当两种处理结果无差别或某种处理不起作用时,理论上差值d的总体均数 $μ_d=0$
• 可将配对设计资料的假设检验视为样本均数与总体均数 $μ_d =0$ 的比较,据定理:
$$ t=\frac{\overline{d}-\mu_d}{s_{\overline{d}}}=\frac{\overline{d}-0}{s_d/\sqrt{n}}=\frac{\overline{d}}{s_d/\sqrt{n}}\sim{t(n-1)} $$
将大白鼠配成8对,每对分别饲以正常饲料和缺乏维生素E饲料,测得两组大白鼠肝中维生素A的含量,试比较两组大白鼠中维生素A的含量有无差别。
| 大白鼠配对号 | 正常饲料组 | 维生素E缺乏组 | 差数d |
|---|---|---|---|
| 1 | 3550 | 2450 | 1100 |
| 2 | 2000 | 2400 | -400 |
| 3 | 3000 | 1800 | 1200 |
| 4 | 3950 | 3200 | 750 |
| 5 | 3800 | 3250 | 550 |
| 6 | 3750 | 2700 | 1050 |
| 7 | 3450 | 2500 | 950 |
| 8 | 3050 | 1750 | 1300 |
| Mean | 3318.75 | 2506.25 | 812.5 |
-
建立检验假设和确定检验水准
$H_0: \mu_d =0,H1: \mu_d ≠0,\alpha=0.05$,双侧检验;
-
选定检验方法和计算统计量
$$ \overline{d}=\frac{\sum d}{n}=\frac{6500}{8}=812.5(U/g) $$
$$ S_{\overline{d}}=\frac{S_d}{\sqrt{n}}=\sqrt{\frac{7370000-(6500)^2/8}{8\times(8-1)}}=193.1298(U/g) $$
$$ t=\frac{\overline{d}-\mu_d}{S_d-\sqrt{n}}=\frac{812.5-0}{193.1298}=4.2070, v=8-1-=7 $$
-
确定p值和作出推断结论
查t分布表(双侧),$ t=4.2>t _{0.05/2, 7} =2.365,p<0.05$。按$ \alpha= 0.05$水准,拒绝$H_0$ ,接受 $H_1$ ,可以认为两种饲料喂养的两组大白鼠中维生素A的含量有差别。正常饲料组比缺乏维生素E饲料组的含量要高。