前序遍历
前序遍历首先访问根节点,然后遍历左子树,最后遍历右子树。
迭代解法
实际上迭代解法分两种形式:
形式一:模拟栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> ans;
if (!root) return ans;
stack<TreeNode*> st;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
st.pop();
ans.emplace_back(node->val);
// 注意模拟栈时,首先出栈的要先入栈
if (node->right) st.push(node->right);
if (node->left) st.push(node->left);
}
return ans;
}
};
|
形式二:通用框架
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> ans;
if (root == nullptr) return ans;
stack<TreeNode*> st;
TreeNode* node = root;
while (!st.empty() || node != nullptr) {
// 先往左走,走到底了就往右,接着重复同样操作
while (node != nullptr) {
ans.emplace_back(node->val);
st.emplace(node);
node = node -> left;
}
node = st.top();
st.pop();
node = node -> right;
}
return ans;
}
};
|
递归解法
更简单,更易于理解,但不容易体现技术水平
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> ans;
if (root == nullptr) return ans;
dfs(root, ans);
return ans;
}
void dfs(TreeNode* node, vector<int>& ans) {
if (!node) return;
// 先写操作,后遍历左右子树
ans.emplace_back(node->val);
dfs(node->left, ans);
dfs(node->right, ans);
}
};
|
中序遍历
中序遍历是先遍历左子树,然后访问根节点,然后遍历右子树。
通常来说,对于二叉搜索树,我们可以通过中序遍历得到一个递增的有序序列。
迭代解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public:
vector<int> midorderTraversal(TreeNode* root) {
vector<int> ans;
if (root == nullptr) return ans;
stack<TreeNode*> st;
TreeNode* node = root;
while (!st.empty() || node != nullptr) {
// 先往左走,走到底了就往右,接着重复同样操作
while (node != nullptr) {
st.emplace(node);
node = node -> left;
}
node = st.top();
st.pop();
ans.emplace_back(node->val);
node = node -> right;
}
return ans;
}
};
|
递归解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution {
public:
vector<int> midorderTraversal(TreeNode* root) {
vector<int> ans;
if (root == nullptr) return ans;
dfs(root, ans);
return ans;
}
void dfs(TreeNode* node, vector<int>& ans) {
if (!node) return;
dfs(node->left, ans);
// 先遍历左子树,再进行操作,再遍历右子树
ans.emplace_back(node->val);
dfs(node->right, ans);
}
};
|
后序遍历
值得注意的是,当你删除树中的节点时,删除过程将按照后序遍历的顺序进行。 也就是说,当你删除一个节点时,你将首先删除它的左节点和它的右边的节点,然后再删除节点本身。
另外,后序在数学表达中被广泛使用。 编写程序来解析后缀表示法更为容易。
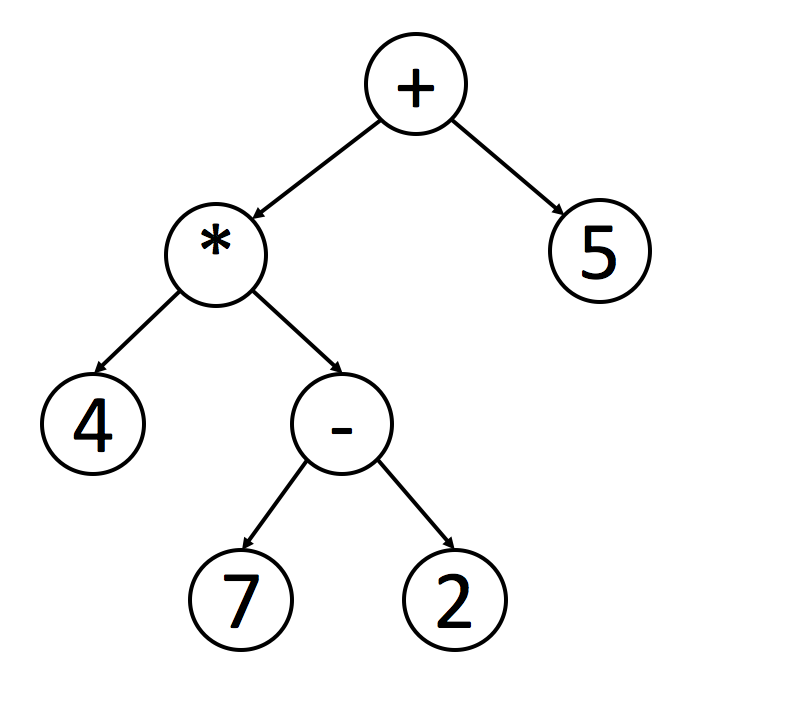
如上图,您可以使用中序遍历轻松找出原始表达式。 但是程序处理这个表达式时并不容易,因为你必须检查操作的优先级。
如果你想对这棵树进行后序遍历,使用栈来处理表达式会变得更加容易。 每遇到一个操作符,就可以从栈中弹出栈顶的两个元素,计算并将结果返回到栈中。
迭代解法
方法一:反前序迭代再反向输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
deque<int> ans;
if (root == nullptr) return ans;
stack<TreeNode*> st;
TreeNode* node = root;
while (!st.empty() || node != nullptr) {
// 先往右走,走到底了就往左,接着重复同样操作
while (node != nullptr) {
ans.emplace_front(node->val);
st.emplace(node);
node = node -> right;
}
node = st.top();
st.pop();
node = node -> left;
}
return ans;
}
};
|
方法二: 硬迭代(较难)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
class Solution {
public:
vector<int> traversal(TreeNode* root) {
vector<int> ans;
// 特例判定
if (root == nullptr) return ans;
stack<TreeNode*> st;
// 当前结点初始化为根节点
TreeNode* node = root;
// prev为记录的前继结点
TreeNode* prev = nullptr;
// 循环判断栈非空 或者 当前结点为空
while (!st.empty() || node != nullptr) {
// 先往左走,走到底了就往右,接着重复同样操作
while (node != nullptr) {
st.emplace(node); // 入栈
node = node -> left; // 继续往左下迭代
}
node = st.top();
st.pop(); // 出栈
// 以下if判断为后序遍历特有的
// 当前结点右子树为空(之前已经入栈了,等于是也遍历完了左右子树了)或刚从右子树上来
if (!node->right || node->right == prev) {
ans.emplace_back(node->val);
// 更新前继结点为当前结点
prev = node;
// node已经访问过了,现在往上走,为了防止node被压入栈,所以要置空
node = nullptr;
} else {
// 从左边上来的时候,往右下角走之前也要入栈
st.emplace(node);
node = node -> right; // 往右子树走一次
}
}
return ans;
}
};
|
递归解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> ans;
if (root == nullptr) return ans;
dfs(root, ans);
return ans;
}
void dfs(TreeNode* node, vector<int>& ans) {
if (!node) return;
dfs(node->left, ans);
// 先遍历左子树,再进行操作,再遍历右子树
dfs(node->right, ans);
ans.emplace_back(node->val);
}
};
|
层次遍历(广度优先)
此种方法区别于其他的方法的地方,在于其为广度优先搜索,适用于一些树的高度或路径记录的问题,需要用到队列来保存候选结点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ans;
if (!root) return ans;
// 定义一个队列
queue<TreeNode*> que;
// 初始加入根节点
que.emplace(root);
// 可用于计算层数
int level = 0;
while (!que.empty()) {
// 先记录队列中元素数量,即当前层元素数量
int size = que.size();
vector<int> temp;
// 当前层每个元素从队列头部出队后加入其左右的非空子结点
for (int i = 0; i < size; ++i) {
TreeNode* cur = que.front();
que.pop();
temp.emplace_back(cur -> val);
if (cur -> left) que.emplace(cur -> left);
if (cur -> right) que.emplace(cur -> right);
}
// 将当前层的所有元素加入结果数组
ans.emplace_back(temp);
}
return ans;
}
};
|
Morris遍历
本方法适用于前序和中序遍历和后序遍历
morris遍历的思想是,通过记忆当前遍历节点的前继节点,建立一个回溯的通道,避免了栈的开销,空间复杂度为常数级。其原理如下代码注释所示
Morris遍历也有中序版本,只需要将对当前节点的操作放到已经遍历完左子树节点的位置即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
class Solution {
public:
vector<int> traversal(TreeNode* root) {
vector<int> ans;
if (!root) return ans;
// 初始化迭代指针p1, p1始终指向需要进行操作的结点
TreeNode* p1 = root;
// p2 指针指向p1的前继结点, 一般为p1的左子树的最右下角的结点
TreeNode* p2 = nullptr;
// 终止条件为 p1 非空
while (p1 != nullptr) {
// p2 初始化为p1的左子树根节点
p2 = p1->left;
// p2 非空, 才要遍历左子树,否则直接遍历右子树
if (p2 != nullptr) {
// p2 往右下角一直走,直到其指向最右下角的结点
while (p2 -> right != nullptr && p2 -> right != p1)
p2 = p2 -> right;
// p2 没有后继(p2->right)结点, 那么改变其后继为p1
if (p2 -> right == nullptr) {
// 前序遍历的操作位置在这里!!!!!!!
ans.emplace_back(p1 -> val);
// 建立 p1 的前继结点
p2 -> right = p1;
// p1 向左下角继续遍历
p1 = p1 -> left;
continue;
} else {
// p2 的后继为 p1, 说明已经遍历过了当前节点的左子树
// 那么将这种关系删除,恢复原状,接着遍历右子树
// 中序遍历 操作的位置在这里!!!!!!
p2->right = nullptr;
p1 = p1 -> right;
}
} else {
// p2 为空,那么直接对当前遍历结点 p1 操作,然后遍历右子树
ans.emplace_back(p1 -> val);
p1 = p1 -> right;
}
}
return ans;
}
};
|
通用框架
迭代解法之先入栈法(前、中序统一)
核心思想为:
-
每拿到一个 节点 就把它保存在 栈 中
-
继续对这个节点的 左子树 重复 过程1,直到左子树为 空
-
因为保存在 栈 中的节点都遍历了 左子树 但是没有遍历 右子树,所以对栈中节点 出栈 并对它的 右子树 重复 过程1
-
直到遍历完所有节点
前序和中序的统一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
class Solution {
public:
vector<int> traversal(TreeNode* root) {
vector<int> ans;
// 特例判定
if (root == nullptr) return ans;
stack<TreeNode*> st;
// 当前结点初始化为根节点
TreeNode* node = root;
// 循环判断栈非空 或者 当前结点为空
while (!st.empty() || node != nullptr) {
// 先往左走,走到底了就往右,接着重复同样操作
while (node != nullptr) {
// 前序操作插入位置
st.emplace(node); // 入栈
node = node -> left; // 继续往左下迭代
}
node = st.top();
st.pop(); // 出栈
// 中序操作插入位置
node = node -> right; // 往右子树走一次
}
return ans;
}
};
|
上述解法的后序遍历需要一些额外的操作,需要记录一个前继结点
后序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
class Solution {
public:
vector<int> traversal(TreeNode* root) {
vector<int> ans;
// 特例判定
if (root == nullptr) return ans;
stack<TreeNode*> st;
// 当前结点初始化为根节点
TreeNode* node = root;
// prev为记录的前继结点
TreeNode* prev = nullptr;
// 循环判断栈非空 或者 当前结点为空
while (!st.empty() || node != nullptr) {
// 先往左走,走到底了就往右,接着重复同样操作
while (node != nullptr) {
st.emplace(node); // 入栈
node = node -> left; // 继续往左下迭代
}
node = st.top();
st.pop(); // 出栈
// 以下if判断为后序遍历特有的
// 当前结点右子树为空(之前已经入栈了,等于是也遍历完了左右子树了)或刚从右子树上来
if (!node->right || node->right == prev) {
ans.emplace_back(node->val);
// 更新前继结点为当前结点
prev = node;
// node已经访问过了,现在往上走,为了防止node被压入栈,所以要置空
node = nullptr;
} else {
// 从左边上来的时候,往右下角走之前也要入栈
st.emplace(node);
node = node -> right; // 往右子树走一次
}
}
return ans;
}
};
|
迭代解法之先出栈法( 前、后序统一)
这里的后序还是采用的逆前序入栈在逆序输出的方式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> result;
if (root == NULL) return result;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
st.pop();
result.push_back(node->val);
if (node->left) st.push(node->left); // 相对于前序遍历,这更改一下入栈顺序 (空节点不入栈)
if (node->right) st.push(node->right); // 空节点不入栈
}
reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了
return result;
}
};
|
中序遍历的方式通过插入空结点作为标记
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
// 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中
st.pop();
// 添加右节点(空节点不入栈)
if (node->right) st.push(node->right);
// 添加中节点
st.push(node);
// 中节点访问过,但是还没有处理,加入空节点做为标记。
st.push(NULL);
// 添加左节点(空节点不入栈)
if (node->left) st.push(node->left);
} else {
// 只有遇到空节点的时候,才将下一个节点放进结果集
// 将空节点弹出
st.pop();
// 重新取出栈中元素
node = st.top();
st.pop();
// 加入到结果集
result.push_back(node->val);
}
}
return result;
}
};
|
递归解法 (前、中、后序统一)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
```cpp
class Solution {
public:
vector<int> traversal(TreeNode* root) {
// 定义返回集
vector<int> ans;
// 进行特殊条件判断
if (root == nullptr) return ans;
// 调用递归函数
dfs(root, ans);
return ans;
}
void dfs(TreeNode* node, vector<int>& ans) {
// 递归终止条件
if (!node) return;
// 前序操作插入位置
dfs(node->left, ans);
// 中序操作插入位置
dfs(node->right, ans);
// 后序操作插入位置
}
};
|
Morris解法(前、中序统一)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
class Solution {
public:
vector<int> traversal(TreeNode* root) {
vector<int> ans;
if (!root) return ans;
// 初始化迭代指针p1, p1始终指向需要进行操作的结点
TreeNode* p1 = root;
// p2 指针指向p1的前继结点, 一般为p1的左子树的最右下角的结点
TreeNode* p2 = nullptr;
// 终止条件为 p1 非空
while (p1 != nullptr) {
// p2 初始化为p1的左子树根节点
p2 = p1->left;
// p2 非空, 才要遍历左子树,否则直接遍历右子树
if (p2 != nullptr) {
// p2 往右下角一直走,直到其指向最右下角的结点
while (p2 -> right != nullptr && p2 -> right != p1)
p2 = p2 -> right;
// p2 没有后继(p2->right)结点, 那么改变其后继为p1
if (p2 -> right == nullptr) {
// !!!!!!!前序遍历的操作位置在这里!!!!!!!!
// 【ans.emplace_back(p1 -> val);】
// 建立 p1 的前继结点
p2 -> right = p1;
// p1 向左下角继续遍历
p1 = p1 -> left;
continue;
} else {
// p2 的后继为 p1, 说明已经遍历过了当前节点的左子树
// 那么将这种关系删除,恢复原状,接着遍历右子树
// !!!!!!!!中序遍历 操作的位置在这里!!!!!!
// 【ans.emplace_back(p1 -> val);】
p2->right = nullptr;
p1 = p1 -> right;
}
} else {
// p2 为空,那么直接对当前遍历结点 p1 操作,然后遍历右子树
ans.emplace_back(p1 -> val);
p1 = p1 -> right;
}
}
return ans;
}
};
|
后序解法需要做一些修改:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
class Solution {
public:
void addPath(vector<int> &vec, TreeNode *node) {
int count = 0;
while (node != nullptr) {
++count;
vec.emplace_back(node->val);
node = node->right;
}
reverse(vec.end() - count vec.end());
}
vector<int> postorderTraversal(TreeNode *root) {
vector<int> res;
if (root == nullptr) {
return res;
}
TreeNode *p1 = root, *p2 = nullptr;
while (p1 != nullptr) {
p2 = p1->left;
if (p2 != nullptr) {
while (p2->right != nullptr && p2->right != p1) {
p2 = p2->right;
}
if (p2->right == nullptr) {
p2->right = p1;
p1 = p1->left;
continue;
} else {
p2->right = nullptr;
addPath(res, p1->left);
}
}
p1 = p1->right;
}
addPath(res, root);
return res;
}
};
|
